SOUND RECORDING
The sound recording is linked to the need to convert the air vibration (which as we have seen reach our ears and are the sound stimulus) into electrical signals. Conversely, the sound reproduction is the conversion of electrical signals into proper vibration of the air.
The instruments you need to sound recording start form a microphone to be then stored on a storage device such as the old magnetic tape, or in the form of small troughs as in old records. Such mode recording of electrical signals is said analogic.
A microphone is a transducer that receives energy from the air vibrations and converts it into energy to electrical oscillations.
Microphones can be of various kinds:
- Condenser
- Piezoelectric
- Electromagnetic
Conversely, reproduction occurs through analogic information reading from a tape, or from the microscopic grooves of the record player, the signal preamp, the amplification and the sending to the speakers that put air into into vibration.
From the analogic mode to digital recording and reproduction. The storage support are still of magnetic type (tapes or magnetic disks) or in the form of small notches how it is on CD or DVD. Compared to the analogic recording mode of the past years, digital information storage aims at numeric information formed of groups of bits.
Therefore, in the above list of needed recording instruments, you need to enter during the registration phase, after the receiving of the signal from the microphone and preamplifier, a signal converter from analogic to digital, which is usually abbreviated with A / D letters. The signal converted into numerical is then filed.
During the reproduction phase, a numerical signal reader and a digital-to- analogic converter (D / A) are required, to continue, as described above, the amplification of the signal to be sent to the speakers.
CONVERSION FROM ANALOGIC TO DIGITAL
The conversion process involves two basic operations:
- The analogic signal sampling
- The numerical coding.
For the sampling of a sound signal from analogical to digital it’s first of all necessary to arrange the division of time in small intervals at constant distance. At each fixed interval, the amplitude of the corresponding signal is measured and deducted. Both the number of divisions of time and the possible values amplitude to be filed, must be chosen with reference to the frequency and amplitude of the signal to be sampled, as well as to the greater or lesser needed accuracy in the inverse phase reproduction phase.
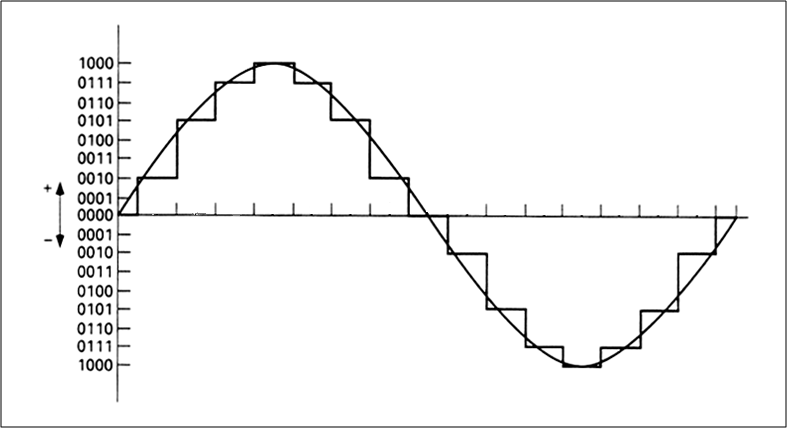
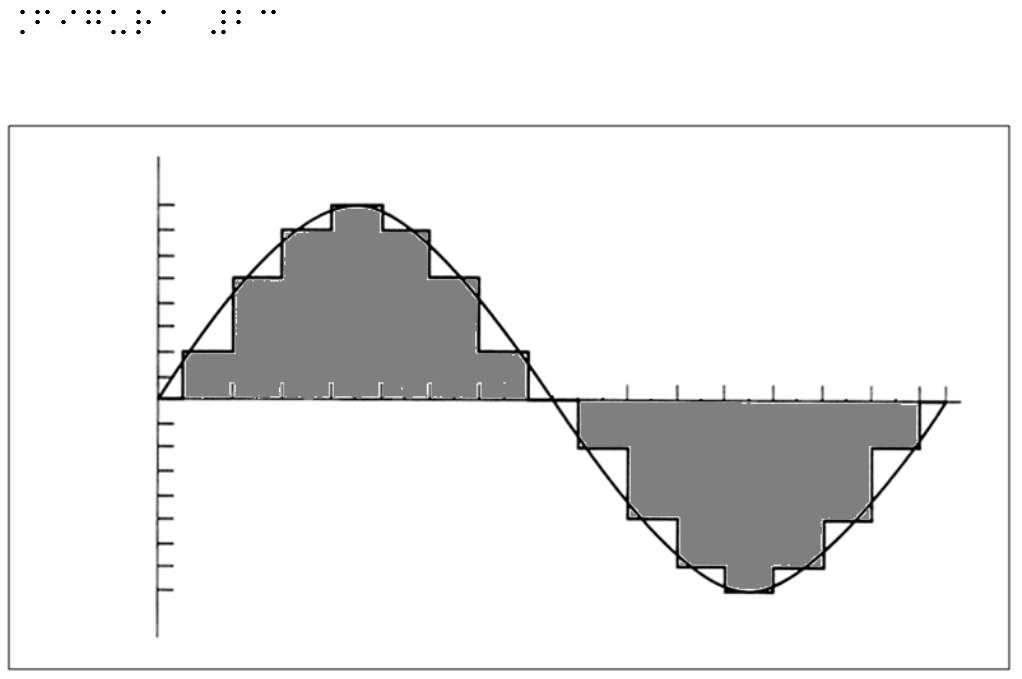
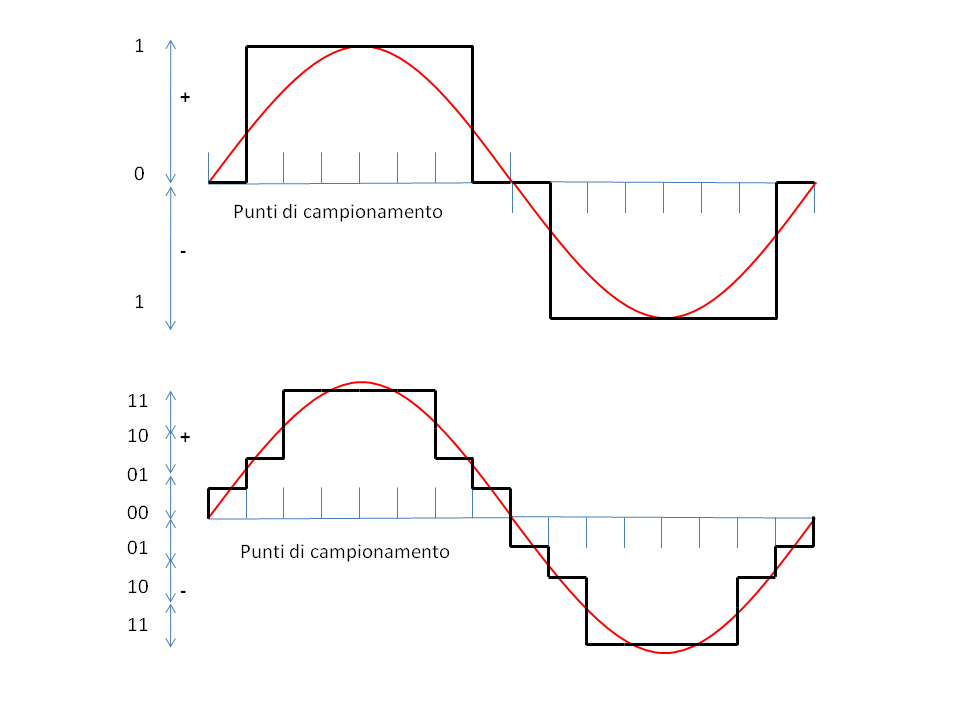
The two above described operations can be considered in a graphical representation on Cartesian axes. In Figure 23, on the x-axis (the time axis) we indicated 16 subdivisions, while on the y- axis, 8 divisions for positive and 8 for negative values of amplitude. For each time division there is the corresponding amplitude, a value that will stay stable for all interval duration and may only vary when next interval will be over.
On the original wave some more marked reference points were identified. The wave obtained by sampling will have a typical ladder form as it can be observed in Figure 23.
 |
 |
| Figure 23 | Figure 23 for embossed printing |
THE CHOICE OF SAMPLING FREQUENCY
The first of the two values to consider is the time division to record the wave amplitude. This value is called sampling frequency, and it is a value that must be chosen in an appropriate way for a correct interpretation of the analogical signal to be converted.
The Nyquist theorem shows that it is necessary to use a sampling frequency of at least twice the highest frequency present in the signal to be sampled. Only in this case it is possible to observe at, if not so much the waveform accuracy, at least its frequency.
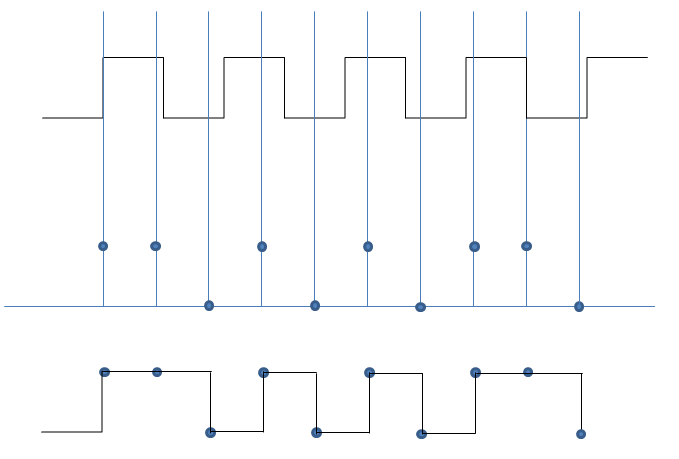
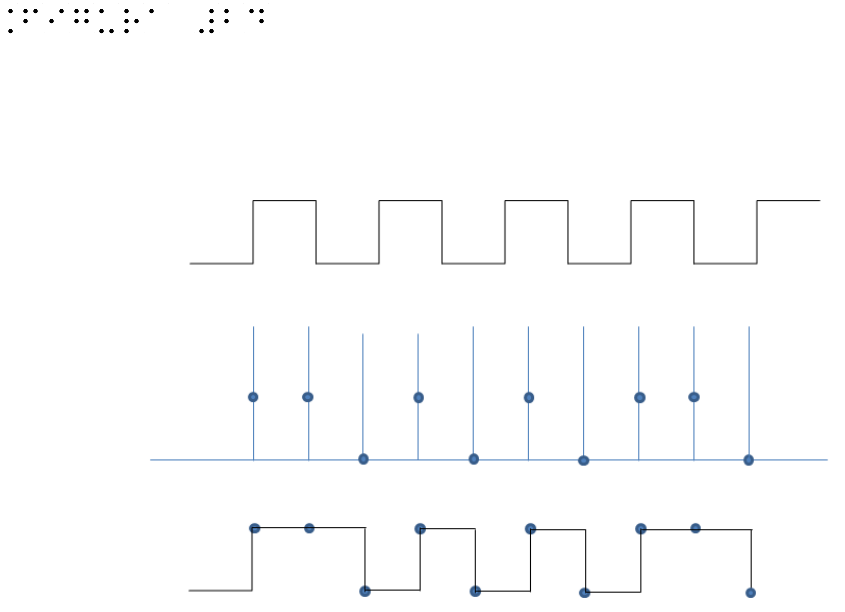
Figure 24 shows an example in which the sampling frequency is insufficient to reconstruct the input signal. The signal consists of 4 waves, with 4 positive and 4 negative peaks. The samples of the figure are only 6 that reproduce a inadequate waveform if compared to the original form.
 |
 |
| Figure 24 | Figure 24 for embossed printing |
The audibility range does not exceed 20 000 Hz, and therefore the value of the required sampling frequency must at least be double of that value. The standard used for CD recording is 44,100 Hz. In terms of time they correspond to sequences of 22.7 microseconds, i.e. the time difference between two samplings is 22.7 microseconds.
The conversion from analogic to digital signal can produce the hearing of altered signals.
If you produce a beat between the sampling frequency and a sampled frequency you can have the “aliasing” phenomenon, i.e. the appearance of a spurious frequency signal equivalent to the difference between the two frequencies.
A very common example of aliasing in a visual field is when sometimes you see in a film the wheels of cars turning in the opposite direction. This spurious signal will overlap the real signal when the sampling frequency is at least twice the highest frequency present in the signal. The example of Figure 24 clarifies why it is appropriate that the sampling frequency is more than twice the maximum of the perceptible frequency.
It is also appropriate to introduce into a converting system an antialiasing filter, to eliminate the unwanted effect of any silent harmonic overtones.
The second considered value besides sampling frequency is the definition of the sample amplitude encoding.
The example of Figure 25 shows that for the same sampling frequency, the waveform reproduces in the most appropriate way if the possible samples values increase. The first picture shows the waveform with only two possible values (0 and 1 that is a bit for the values and a bit for the sign) and the same form with four possible positive and negative values (i.e. from 0 to 3 that is 2 bits for the values and a bit for the sign).
 |
 |
| Figure 25 | Figure 25 for embossed printing |
Using appropriate sampling values is crucial to ensure the quality of what is called "dynamic" of sound and music that can go from pianissimo to fortissimo with a climb that can reach over 70-80 dB. The fixed limit (in theory) for CDs is 96dB. A suitable encoding, bearing in mind that also the sign that is to subtract a bit must be represented, must be at least of 16 bits, i.e. 2^16 that correspond to 65,536 values, i.e. a scale running from -32768 to +32768. The 16-bit value is used as standard for audio CDs, while other formats such as audio DVD support a depth up to 24 bits.
Considering that the connection between the depth (i.e. the values indicated in bits) and the dynamic interval (indicated in dB) may be approximately indicated with the ratio of 1/6, it follows that increasing the definition of a bit, the dynamic increases by about 6 dB. So, with 16-bit you can get a dynamic that in theory is of 16 * 6 which is 96 dB, while with 24 bits it is possible to obtain a dynamic that in theory is of 24 * 6 or about 144 dB.
If you use a low resolution and quantization value for a weak intensity signal, there will be a typical quantization noise that would be annoying when amplified. The following example presents a piano sound that when fading shows the typical quantization noise.
SOUND SAMPLE
The following pictures have the same signal that keeps the sample resolution value to 16 bits, and reduces the sampling frequency values to 44.100 Hz, the second to 22050 Hz, the third to 11025 Hz and finally the last to 8000 Hz. The waveform gradually loses its form to be reduced to a simpler wave.
 |
 |
| Figure 27 | Figure 27 for embossed printing |
Listening to a music example (the opening part of violin and strings concert by Mendelssohn) makes the most of the original fidelity signal falling-off.
| 44100Hz and 16 bits example | 22050Hz and 16 bits example |
| 11025Hz and 16 bits example | 8000Hz and 16 bits example |
| 3000Hz and 16 bits example |
Below it is graphically represented the same signal in which the sampling frequency is maintained at 44.100 Hz, but the resolution is reduced from 16 to 8 bits.
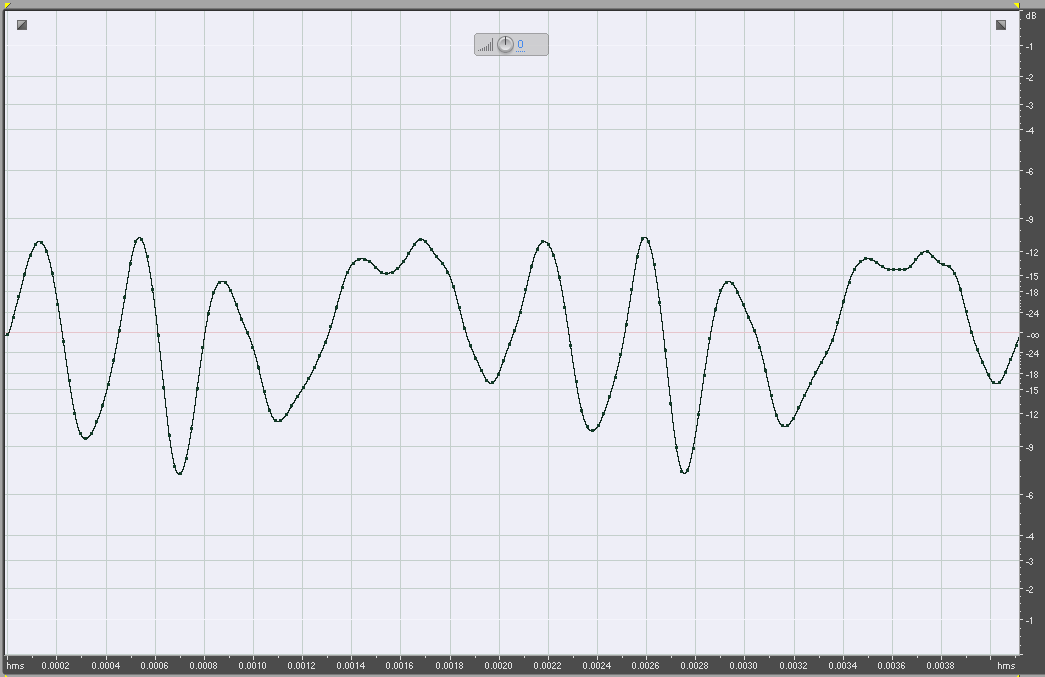
Violin 44100Hz 16 bit
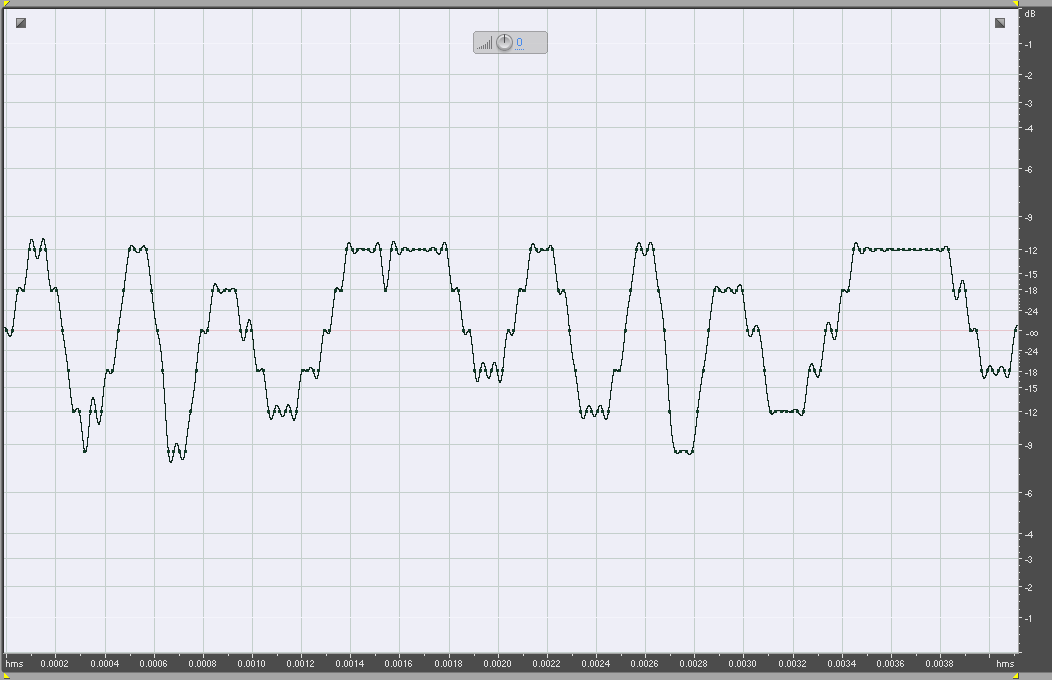
Violin 44100Hz 8 bit
Listening to the following examples for the three resolution values (16, 8 and 4 bits) makes the most of the original fidelity signal falling-off.
| 44100Hz and 16 bits example | 44100Hz and 8 bits example |
| 44100Hz and 4 bits example |
The dimensions in byte values to record one-hour music quality as that of CDs are very high and correspond to 44.100 Hz of sampling frequency and 16 bits of resolution that for stereophony have to be duplicates and that correspond to the followings:
16 (resolution bits) * 44100 (sampling frequency) * 3600 (seconds) * 2 (stereo channels) = 5,08 E +09 bits. This value, expressed in Mbytes (knowing that 8 bits correspond to a byte) corresponds to 635.04 Mbytes. The CD contains audio data plus other information, such as error correction and other general type as track number, passed time, song title, etc.
