PERIODICAL COMPLEX WAVE
Let’s now examine more closely a wave called “periodical" because it is repeated over time in constant form. Figure 9 shows a periodical complex wave, while figure 10 represents a sinusoidal wave.
 |
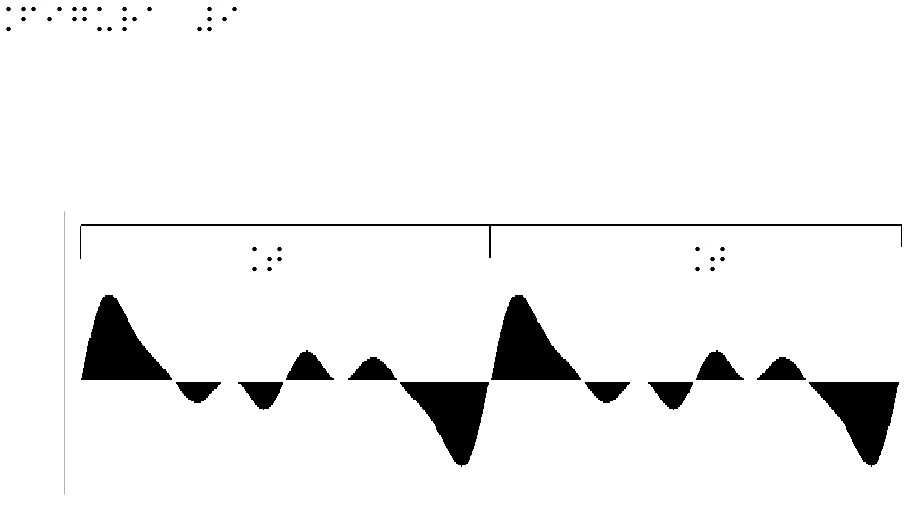 |
| Figure 9 | Figure 9 for embossed printing |
 |
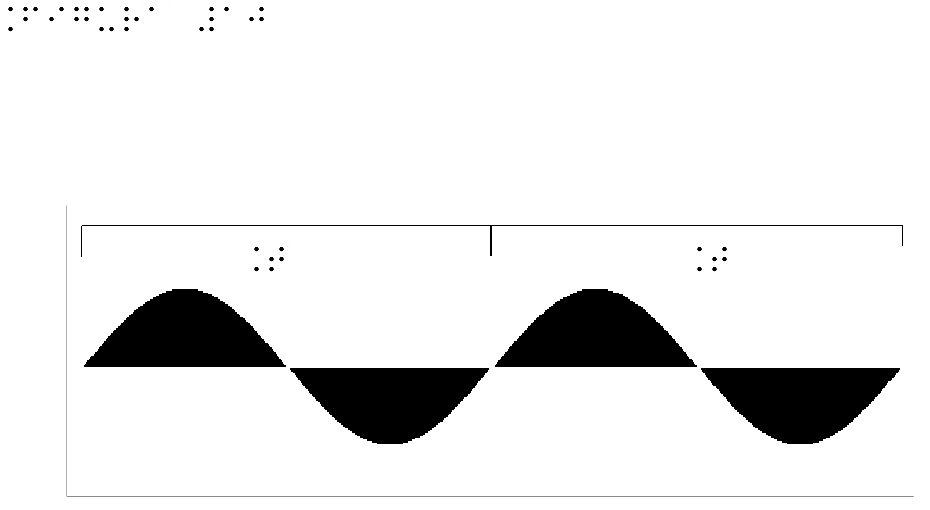 |
| Figure 10 | Figure 10 for embossed printing |
As already told, the vertical axis (ordinate) always indicates the wave amplitude or intensity, while the horizontal axis (abscissa) indicates time. As Figure 10 shows, a sinusoidal wave always has one positive and one impulse.
The period is the duration of a complete oscillation cycle (by citing the pendulum round trip) and it is indicated by the capital letter T, in other words, it is the time that elapses between two successive repetitions.
The wavelength is represented by the Greek letter " γ " (range that is indicated into Braille language as the Greek letter " g", i.e. Braille points 1,2,4,5); it is a term widely used in radio frequency and it is the distance of a cycle indicated in metres. The letter " f " indicates the frequency that is the number of oscillations in the unit of time that is intentionally the second minute (commonly called second); frequency is measured in cycles per second (c / s) or, in honour to German physicist Heinrich Rudolf Hertz (1857 - 1894), in hertz (Hz symbol).
There is a close connection between frequency and wavelength. To each wavelength corresponds a frequency and vice versa. For example, the length of the radio waves of an oscillating current of a million cycles per second transmitted from one antenna is:
Length of the radio wave = Propagation speed of the radio wave / Frequency
so
1 = 300,000,000 / 1,000,000 = 300 meters
The connections among period (T), wavelength ( γ ) and propagation speed ( v) are the following:
T = γ / v or v = γ / T
Even between period and frequency there is a close connection, because the higher is the frequency proportionately the smaller is the period (and wavelength) and vice versa, i.e., the lower is the frequency, the greater are the period and the wavelength.
Translating with a small formula, we have:
f = 1 / T or T = 1 / f
The period T is also the time it takes to a given wavelength disturbance to pass through a given point in space. Let’s assume that taken time is 0.25 seconds: you will have in this case a frequency of 4 Hz.
In fact:
f = 1 / T = 1 / 0, 25 = 4 Hz
From the above-mentioned formulas we can assume that:
v = γ * f
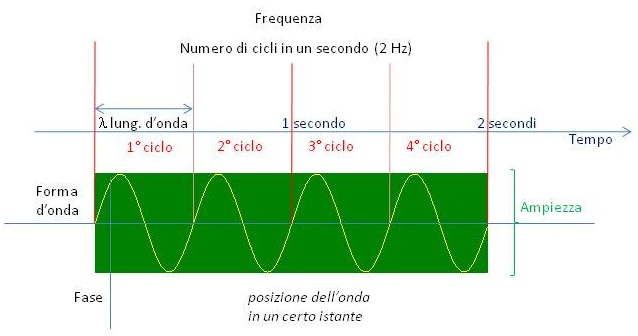
Figure 11 summarizes all the variables of a simple harmonic motion.
 |
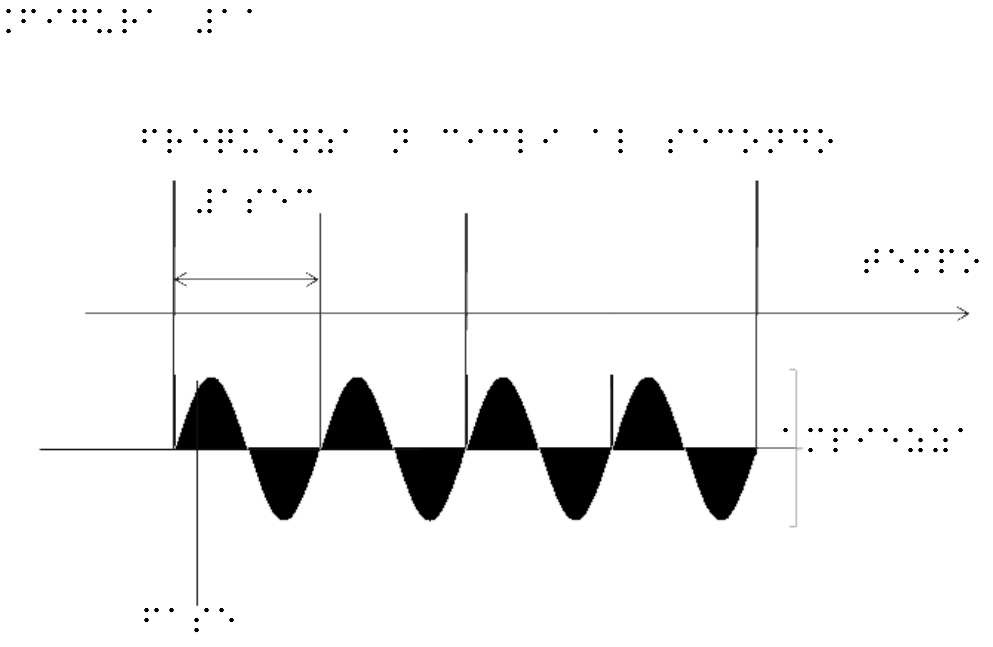 |
| Figure 11 | Figure 11 for embossed printing |
The wave speed propagation is a constant depending on the mean and not by the wavelength, except in special cases, sometimes negligible, as the light reflecting into water or glass.
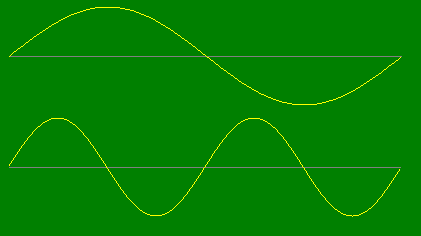
Figure 12 shows the representations of two equal amplitude sinusoids, but different in frequency (one is the double of the other) and consequently different in periods (one is the half of the other).
 |
 |
| Figura 12 | Figure 12 for embossed printing |
