8.1 The construction of scales
The term scale indicates a series of sounds sorted in ascending or descending order of pitch, starting from any note and continuing until it reaches the octave above or below. The scale should be understood as a series of steps, and for this we have to imagine the piano keyboard as a series of equally spaced pitches. The difference between one pitch and its nearest neighbour is called a semitone.
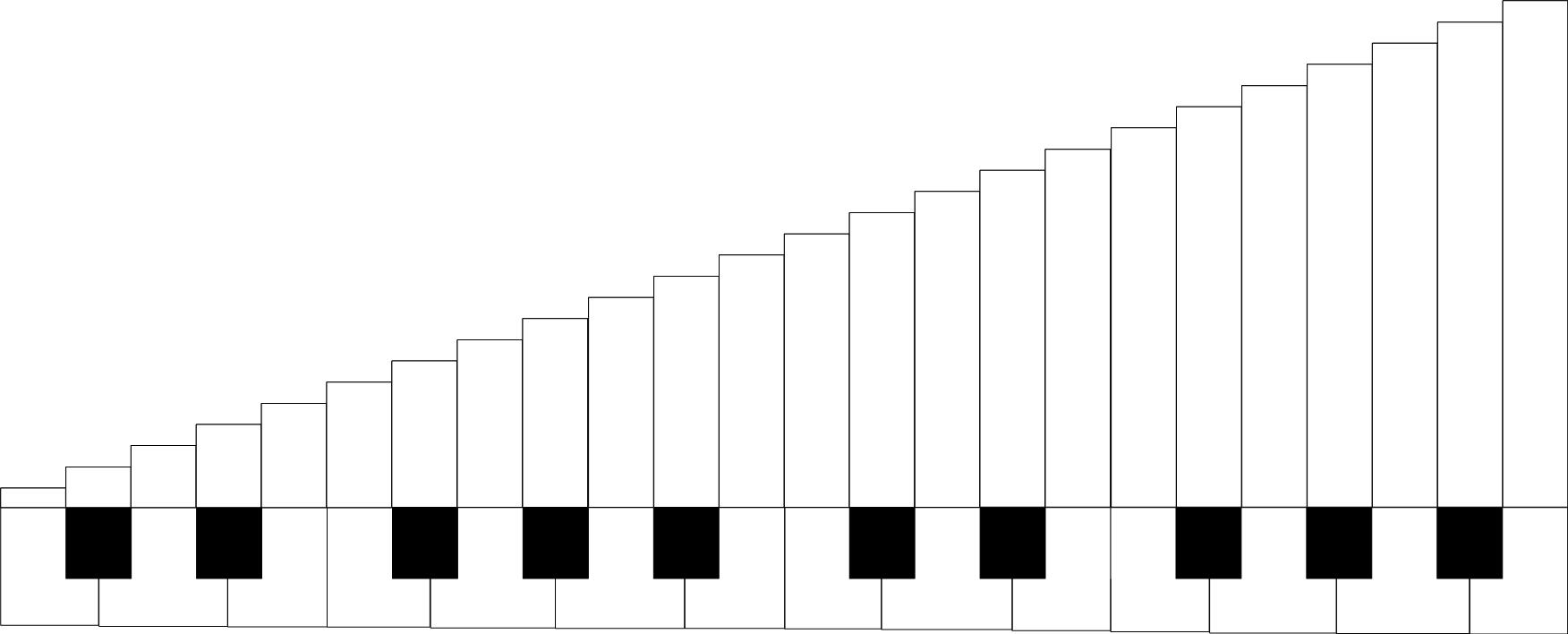
There are several ways to "go up" or "down" a scale. We can play all the steps and, in this case, we will obtain a chromatic scale (a scale composed by semitone intervals). We can go up two steps at a time and we will have a whole-tone scale (scale composed tone intervals), or we can go up using a mixture of tones and semitones. Most commonly used are the diatonic scales - formed from seven sounds that divide the octave into five tones and two semitones arranged in various ways, and never with two consecutive semitones.
8.2 The modes
The different patterns of tones and semitones in which we climb the diatonic scales are known as modes.
In classical music there are two modes: major and minor.
Scales are named according to the note on which they begin and their mode. So, for example, a scale that employs the major mode starting on F is called F major. A scale that employs the minor mode starting on G is called G minor.
The first note of the scale is called the first degree. Each diatonic scale has seven degrees before reaching its octave.
On the sixth degree of each major scale you can start a minor scale (called the relative natural minor) that uses the same sounds.
The diagrams below show the order of intervals in the major and minor modes:
Major mode:

Minor mode:

Listen to a major scale
Listen to a minor scale

Looking at the illustrations above, we can see that in the major scale the semitones fall between the 3rd and 4th degrees and between the 7th degree and the octave, while in the natural minor scale the semitones are located between the 2nd and 3rd degrees and between the 5th and 6th degrees
8.3 The degrees of the scale
Each note of the scale is given a name which reflects its function within the scale.
| I degree | tonic |
| II degree | supertonic |
| III degree | mediant |
| IV degree | subdominant |
| V degree | dominant |
| VI degree | submediant |
| VII degree | leading note |
The 1st degree, or tonic, is of crucial importance because it is the note upon which the scale is based.
The 5th degree, or dominant, is so called because of its very strongly consonant relationship with the tonic. Indeed, after the octave the perfect 5th is the strongest consonance.
The 4th degree, or subdominant, is so called because it is the same distance (a perfect 5th) below the tonic as the dominant is above. "Sub" (from Latin) means "below".
The 3rd degree is known as the mediant because it lies midway in the scale between the tonic and the dominant. Note that this note is important in defining the mode of the scale. If it is a major 3rd then the scale is major. If it is a minor 3rd then the scale is minor.
The 6th degree is known as the submediant because it lies midway in the scale between the subdominant and the tonic. Just as the mediant is the third note up the scale from the tonic so the submediant is the third note down the scale from the tonic.
The name supertonic, given to the 2nd degree of the scale, simply means "above the tonic". "Super" (from Latin) means "above".
Finally, the 7th note of the scale is known as the leading note because it has a strong feeling of leading to the tonic.
8.4 The scales
On each note of the chromatic scale we can build both a major and a minor scale.
Let us look at all the scales (major and relative minor), starting with C major, which has no sharps or flats, and then move on to those that do have sharps or flats. A scale may have up to seven sharps or flats. These are indicated immediately after the clef in what is known as a key signature and they remain constant for the notes of the same name that are encountered in the piece.
It will be noted that the scales are ordered by perfect fifth intervals, both ascending (the scales with sharps) and descending (for those with flats).
The order of major scales with sharps is as follows:
C, G , D, A, E, B, F sharp, C sharp.
The order of major scales with flats is as follows:
F, B flat, E flat, A flat, D flat, G flat, C flat.
The order in which the sharps and flats appear in key signatures is also governed by the interval of the perfect 5th.
For sharps:
F |
C |
G |
D |
A |
E |
B |
Example in braille
For the flats:
B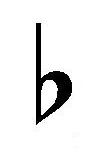 |
E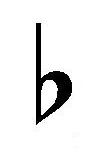 |
A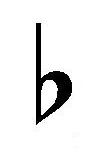 |
D |
G |
C |
F |
Braille example
We list below all the major scales and their relative minors:
Scale of C major and of A minor Example in braille

Scale of G major and of E minor, with key signature (F#). Example in braille

Scale of D major and of B minor, with key signature (F#, C#). Example in braille

Scale of A major and of F# minor, with key signature (F#, C#, G#). Example in braille

Scale of E major and of C# minor, with key signature (F#, C#, G#, D#). Example in braille

Scale of B major and of G# minor, with key signature (F#, C#, G#, D#, A#). Example in braille

Scale of F# major and of D# minor, with key signature (F#, C#, G#, D#, A#, E#). Example in braille

Scale of C# major and of A# minor, with key signature (F#, C#, G#, D#, A#, E#, B#). Example in braille

Scale of F major and of D minor, with key signature (B flat). Example in braille

Scale of B flat major and of G minor, with key signature (B flat, E flat). Example in bbraille

Scale of E flat major and of C minor, with key signature (B flat, E flat, A flat). Example in braille

Scale of A flat major and of F minor, with key signature (B flat, E flat, A flat, D flat). Example in braille

Scale of D flat major and of B flat minor, with key signature (B flat, E flat, A flat, D flat, G flat). Example in braille

Scale of G flat major and of E flat minor, with key signature (B flat, E flat, A flat, D flat, G flat, C flat). Example in braille

Scale of C flat major and of A flat minor, with key signature (B flat, E flat, A flat, D flat, G flat, C flat, F flat). Example in braille

8.5 Enharmonic scales
As can be seen from the examples above there are three major and three minor that can be "spelt" in either sharps or flats. The two spellings of each scale are described as enharmonic.
| B major | is enharmonic with | C flat major |
| G# minor | is enharmonic with | A flat minor |
| F# minor | is enharmonic with | G flat major |
| D# minor | is enharmonic with | E flat minor |
| C# minor | is enharmonic with | D flat major |
| A# minor | is enharmonic with | B flat minor |
8.6 How to identify the key
For sharp keys, the last sharp in the key signature is the leading note of the major scale. The tonic is a semitone above this note.
For flat keys, the tonic of the major scale is the penultimate flat in the key signature. Of course, for F major there is no penultimate flat in the key signature but it is easy to remember that F major is the key with one flat for its key signature
8.7 Scales with double sharps or flats
In addition to the above keys there are other scales that use double sharps and double flats. In practice these are never written with key signatures but occasionally a piece of music might go into such a key. For example the key of G sharp major (enharmonic with A flat major), is composed of six sharps and a double sharp and this occurs in Bach's C# major Prelude and Fugue from Book 1 of the "48" where the music, having started in 7 sharps, modulates to the dominant adding an extra sharp to the mix
8.8 Minor scales
At this point the minor scales deserve a separate discussion, because they are subject to alteration with respect to their key signatures.
Observing the order of the intervals of the minor scale, it can be noted that, between the 7th degree and the tonic, there is an interval of a tone.
This means that the 7th degree is not technically a leading note, because there is no tendency to lead on to the tonic. As stated earlier, the tendency for the leading note of a major scale to lead to the tonic derives from the fact that it is a semitone away from that tonic. If the 7th degree is therefore sharpened to produce a true leading note then we get the so called harmonic minor scale.
Here is an example of the A harmonic minor scale:

Example in braille
In this scale (which remains unchanged both ascending and descending) there appears a new interval (F - G sharp) of a tone and a half (augmented second), which makes the scale harder to sing. To overcome this problem, the 6th degree of the scale may also be sharpened by a semitone, thus creating the melodic minor scale. This scale, in descending, uses the notes of the natural minor scale (on other words in accordance with the key signature) since the 7th degree of the scale is no longer leading to the tonic but, instead, downwards away from the tonic. With the 7th degree not sharpened there is no need to sharpen the 6th degree either.
Here is an example of the A melodic minor scale:

Example in braille
8.9 Less frequently used scales
Other less frequently used scales exist. Here are some examples:
The mixed minor scale:

Example in Braille
The minor scale used by J. S. Bach:

Example in Braille
The Neapolitan minor scale:

Example in Braille
The harmonic major scale:

Example in Braille
The enigmatic scale of G. Verdi:

Example in Braille
The whole tone scale, formed of six tones, as used, for example, by Debussy:

Example in Braille
8.10 The chromatic scale
The chromatic scale, ascending, is normally spelt using sharps:

While, descending, it will normally be spelt using flats:

Example in Braille
Many more scales exist. Busoni, for example, constructed at least 103 scales
