PROPAGATION OF SOUND
THEORY OF WAVES
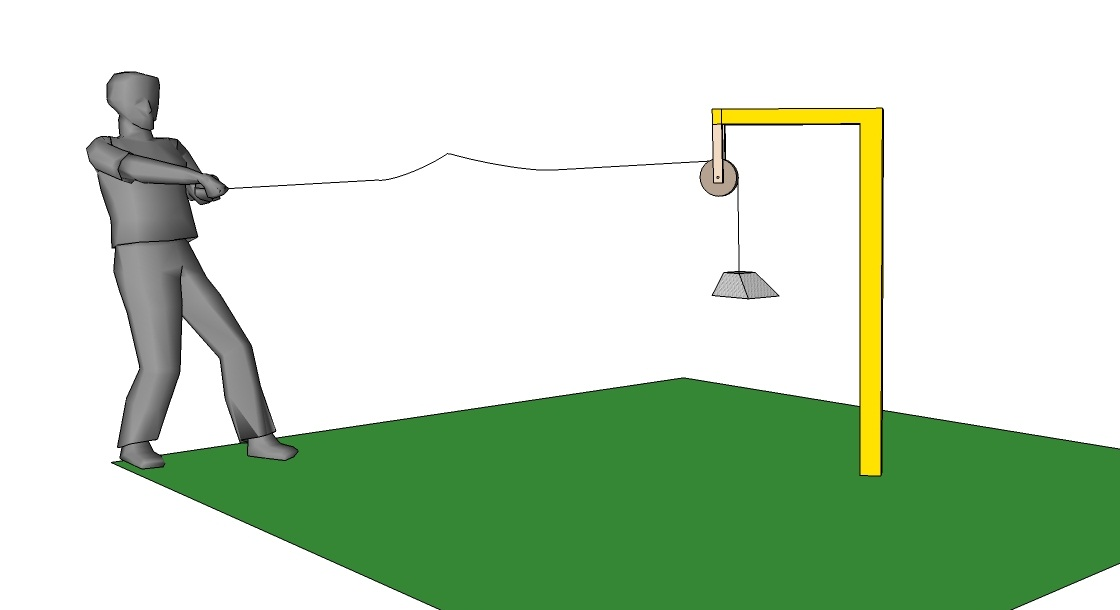
The vibrations of an elastic body in order to reach our ears need a mean that transport and spread the energy produced by the body. When it comes to energy transfer it is natural to think of a mass moving under a thrusting action (for example, the kinetic energy transmitted to the arrow from a bow is transferred to the target). However, it is possible to transfer energy even without mass movement. As a practical example, let’s consider a long elastic cord and let’s secure one end to a pulley which is coupled to a weight; on the opposite side, with the tight cord, with a hand movement let’s generate an impulse which will cover the entire length of the cord and momentarily raise the weight thus producing a work that is more or less equal to the one made to produce the impulse. There has not been mass movement because the cord has stayed in its place as it was at the beginning. The perturbation (i.e. energy), which moves at constant speed along the cord, is the considered wave.
Figure 1 shows a person who, stretching his/her arm, generates a wave on a cord to the end of which, passing through a pulley drawn as a small circle, a weight is attached.
 |
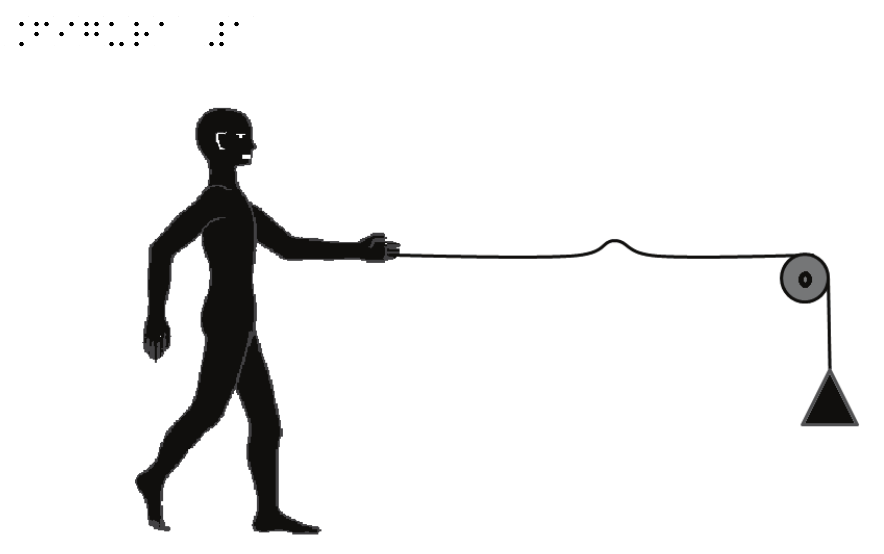 |
| Figure 1 | Figure 1 for embossed printing |
From the just mentioned practical experiment some considerations could be drawn:
- The mean has a precise point of equilibrium or rest;
- The perturbation along the mean moves at a constant speed that depends on the type of mean and not by the amplitude or form of the wave;
- Each point of the cord moves up and down with respect to the rest point at an inconstant speed and at an amplitude that depends on the impulse energy;
- The wave amplitude decreases as it go trough the mean, but it does not slow down its speed.
The cord points move perpendicular to the direction of wave motion, and these waves are called transverses. Let's look more closely at the various positions taken by a point on the cord as an impulse that travels to the right passes by. The point, on its rest position, receives an upward acceleration, and then it keeps on rising with a speed decreasing to zero speed. The same happens in the descending phase in which there is a first acceleration phase and a subsequent deceleration until returning to the rest position. Broadly speaking, we can say that these movements generate the forces that cause movements.
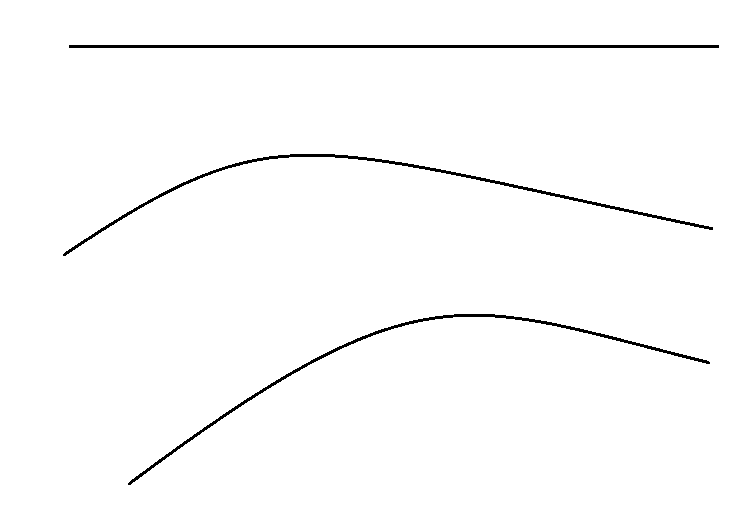
Figure 2 shows a chart showing the cord in three different positions:
- Equilibrium position,
- Frame of the cord movement produced by a wave in a certain instant,
- This third image shows the cord movement compared to the previous picture after just 0.2 milliseconds.
 |
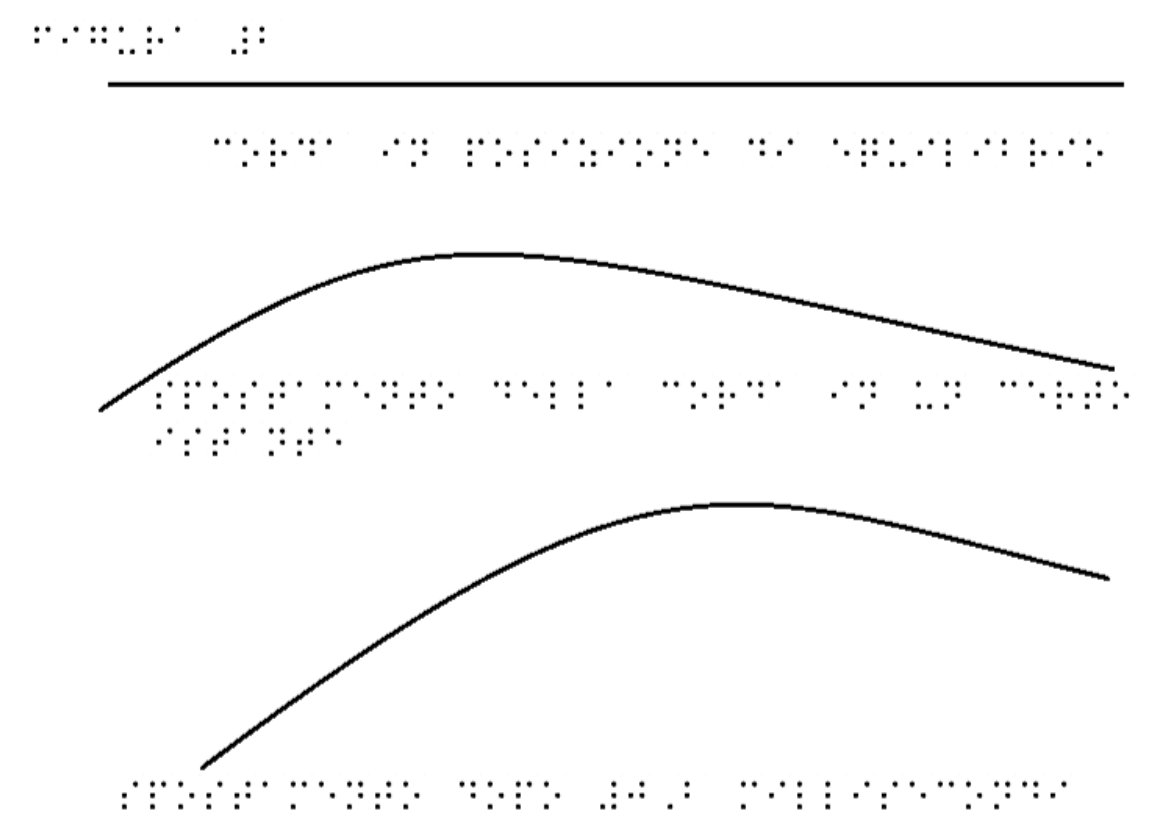 |
| Figure 2 | Figure 2 for embossed printing |
There are also waves that have their oscillations compared to the mean rest point in the longitudinal mode, i.e. in the same direction of wave propagation.
To better understand this aspect, let’s think of a large spring constrained at its extremes and compress it at one end and then leave some of its coils.
These will tend to move toward their rest point, but before they will compress the close coils, before moving to their rest point, will compress the other nearby coils, and so on. There will, therefore, be an unceasing impact compression movement to the other end of the spring. A point on the spring (and more generally in a fluid also), if moved from its equilibrium, receives some forces from the surrounding elements that tend to restore it to its original rest state (Newton’s second aw). At the same time, however, (Newton’s third law) a point moved from its equilibrium exerts a force on the adjacent points of the spring (and more generally on the surrounding matter), and when that point is drawn back toward its equilibrium, it moves out of its equilibrium also the adjacent points.
Figure 3 shows a dashed spring whose first part is at rest, the second is in expansion and the third is in compression until at rest state again.
 |
 |
| Figure 3 | Figure 3 for embossed printing |
The longitudinal and transverse waves can propagate in a solid mean while into fluids (air and water) only longitudinal waves propagate, since the fluid forces on what surrounds are characterized by a single size, which is pressure. A sound that propagates into air and a longitudinal wave alternating compressions to rarefaction. In other words, sound waves are mechanical compression and rarefaction waves.
Let’s now examine the longitudinal air vibrations produced by a plate securely locked to an end. When the plate is motionless, the surrounding air portion does not change its state of rest, when we instead slightly flex (slightly so as not to deform it permanently) the other end of this plate, it will begin to oscillate around its rest point close to creating some compression perturbations and sinusoidal rarefactions, which are transmitted to more distant air portions. Our ear is sensitive to such pressure variations within certain limits we are going to see afterwards.
Figure 4 shows a lateral view representation of the plate in its rest position. The embossed picture shows the plates in a central position with a more marked trait, while the thinner form indicates the left and right plates deflection. At the left and the right of the plate some compression and rarefaction disturbances, designed with curved hatching, are created.

Figure 4
